En esta unidad retomamos el tema de los sistemas de ecuaciones y los diferentes sistemass para resolveros, esto para poder hacer de forma más sencilla los temas que venían más adelante.
Después entramos al tema de matrices, aprendiendo que se pueden sumar, restar y multiplicar con ciertas condiciones, también podemos encontrar los valores de las variables en un sistema de ecuaciones tomando los coeficientes y los resultados en forma de matriz. A éstas también se les puede sacar inversa, pero no en todos los casos era posible. Por último teníamos la opción de poder llegar a los resultados obteniendo primero el determinante de la matriz.
lunes, 30 de noviembre de 2015
4.3 Determinantes
4.3.1 Definición de un determinante.
 = a 11 a 22 − a 12 a 21
= a 11 a 22 − a 12 a 21
 =
=
 =
=












A cada matriz cuadrada A se le asigna un escalar particular denominadodeterminante de A, denotado por |A| o por det (A).
|A| = 

Determinante de orden uno
|a11| = a11
Ejemplo
|5| = 5
Determinante de orden dos
 = a 11 a 22 − a 12 a 21
= a 11 a 22 − a 12 a 21
Ejemplo


Determinante de orden tres
Consideremos una matriz 3x3 arbitraria A = (aij). El determinante de A se define como sigue:
 =
=
= a11 a22 a33 + a12 a23 a 31 + a13 a21 a32 −
− a13 a22 a31 − a12 a21 a 33 − a11 a23 a32.
Obsérvese que hay seis productos, cada uno de ellos formado por tres elementos de la matriz. Tres de los productos aparecen con signo positivo (conservan su signo) y tres con signo negativo (cambian su signo).
Ejemplo
 =
=
3 · 2 · 4 + 2 · (−5) · (−2) + 1 · 0 · 1 −
− 1 · 2 · (−2) − 2 · 0 · 4 − 3 · (−5) · 1 =
= 24 + 20 + 0 − (−4) − 0 − (−15) =
= 44 + 4 + 15 = 63
4.3.2 Expansión por cofactores.
egormaximenko. (2015). Menores y cofactores.Expansión del determinante por cofactores. noviembre 30, 2015, de google Sitio web: http://esfm.egormaximenko.com/linalg/determinant_cofactors_es.pdf
4.3.3 Propiedades de los determinantes.
1 |At|= |A|
El determinante de una matriz A y el de su traspuesta At son iguales.


2 |A| = 0 Si:
Posee dos filas (o columnas) iguales.

Todos los elementos de una fila (o una columna) son nulos.

Los elementos de una fila (o una columna) son combinación lineal de las otras.

F3 = F1 + F2
3 Un determinante triangular es igual al producto de los elementos de la diagonal principal.

4 Si en un determinante se cambian entre sí dos filas (o dos columnas), su valor sólo cambia de signo.


5 Si a los elementos de una fila (o una columna) se le suman los elementos de otra multiplicados previamente por un número real, el valor del determinante no varía.
Es decir, si una fila (o una columna) la transformamos en una combinación lineal de las demás, el valor del determinante no varía.


6 Si se multiplica un determinante por un número real, queda multiplicado por dicho número cualquier fila (o cualquier columna), pero sólo una.

7 Si todos los elementos de una fila (o columna) están formados por dos sumandos, dicho determinante se descompone en la suma de dos determinantes en los que las demás filas (o columnas) permanecen invariantes.

8 |A · B| =|A| · |B|
El determinante de un producto es igual al producto de los determinantes.
4.3.4 Regla de Cramer.
https://www.youtube.com/watch?v=lLPcHVAqY804.2 Álgebra de Matrices
El concepto de matriz alcanza múltiples aplicaciones tanto en la representación y manipulación de
datos como en el cálculo numérico y simbólico que se deriva de los modelos matemáticos
utilizados para resolver problemas en diferentes disciplinas como, por ejemplo, las ciencias
sociales, las ingenierías, economía, física, estadística y las diferentes ramas de las matemáticas
entre las que destacamos las ecuaciones diferenciales, el cálculo numérico y, por supuesto, el
álgebra
4.2.1 Tipos de matrices (cuadrada, rectangular, triangular, matriz identidad, matriz transpuesta).











4.2.2 Operaciones con matrices (suma, diferencia, multiplicación por escalar y producto de matrices).








4.2.1 Tipos de matrices (cuadrada, rectangular, triangular, matriz identidad, matriz transpuesta).
Matriz fila
Una matriz fila está constituida por una sola fila.

Matriz columna
La matriz columna tiene una sola columna

Matriz rectangular
La matriz rectangular tiene distinto número de filas que de columnas, siendo su dimensión mxn.

Matriz traspuesta
Dada una matriz A, se llama matriz traspuesta de A a la matriz que se obtiene cambiando ordenadamente las filas por las columnas.

(At)t = A
(A + B)t = At + Bt
(α ·A)t = α· At
(A · B)t = Bt · At
Matriz nula
En una matriz nula todos los elementos son ceros.

Matriz cuadrada
La matriz cuadrada tiene el mismo número de filas que de columnas.
Los elementos de la forma aii constituyen la diagonal principal.
La diagonal secundaria la forman los elementos con i+j = n+1, siendo n el orden de la matriz.

Tipos de matrices cuadradas
Matriz triangular superior
En una matriz triangular superior los elementos situados por debajo de la diagonal principal son ceros.

Matriz triangular inferior
En una matriz triangular inferior los elementos situados por encima de la diagonal principal son ceros.

Matriz diagonal
En una matriz diagonal todos los elementos que no están situados en la diagonal principal son nulos.

Matriz escalar
Una matriz escalar es una matriz diagonal en la que los elementos de la diagonal principal son iguales.

Matriz identidad o unidad
Una matriz identidad es una matriz diagonal en la que los elementos de la diagonal principal son iguales a 1.

Matriz regular
Una matriz regular es una matriz cuadrada que tiene inversa.
Matriz singular
Una matriz singular no tiene matriz inversa.
Matriz idempotente
Una matriz, A, es idempotente si:
A2 = A.
Matriz involutiva
Una matriz, A, es involutiva si:
A2 = I.
Matriz simétrica
Una matriz simétrica es una matriz cuadrada que verifica:
A = At.
Matriz antisimétrica o hemisimétrica
Una matriz antisimétrica o hemisimétrica es una matriz cuadrada que verifica:
A = −At.
Matriz ortogonal
Una matriz es ortogonal si verifica que:
A . A^t = I
math2me. (2014). Suma y resta de matrices. noviembre 30. 2015, de youtube Sitio web: https://youtu.be/DgQuy_wbVZE
4.2.3 Propiedades de las operaciones con matrices.
Jarne. G, Minguillón. E & Zobal T.. (2015). OPERACIONES CON MATRICES. OROPIEDADES. noviembre 30, 2015, de google Sitio web: http://www.unizar.es/aragon_tres/unidad6/Matrices/u6matte30.pdf
4.2.4 Matriz inversa.
Si premultiplicamos (multiplicamos por la izquierda) o posmultiplicamos (multiplicamos por la derecha) una matriz cuadrada por su inversa obtenemos la matriz identidad.
A · A−1 = A−1 · A = I
Propiedades
1 (A · B)−1 = B−1 · A−1
2 (A−1)−1 = A
3 (k · A)−1 = k−1 · A−1
4 (At)−1 = (A−1)t
Cálculo por el método de Gauss
Sea A una matriz cuadrada de orden n. Para calcular la matriz inversa de A, que denotaremos como A−1, seguiremos los siguientes pasos:
1 Construir una matriz del tipo M = (A | I), es decir, A está en la mitad izquierda de M y la matriz identidad I en la derecha.
Consideremos una matriz 3x3 arbitraria:

La ampliamos con la matriz identidad de orden 3.

2 Utilizando el método Gauss vamos a transformar la mitad izquierda, A, en la matriz identidad, que ahora está a la derecha, y la matriz que resulte en el lado derecho será la matriz inversa: A−1.
F2 = F2 − F1

F3 = F3 + F2

F2 = F2 − F3

F1 = F1 + F2

F2 = (−1) F2

La matriz inversa es:

domingo, 29 de noviembre de 2015
4.1 Sistemas de ecuaciones lineales.
Una gran cantidad de problemas en negocios y economía desembocan en los denominados
sistemas de ecuaciones lineales. Por ejemplo, consideremos la siguiente situación.
El propietario de una tienda de televisores desea expandir su negocio comprando y poniendo a la venta dos nuevos modelos de televisores que acaban de salir al mercado. Cada televisor del primer tipo cuesta $300 y cada televisor del segundo tipo $400. Cada televisor del primer tipo ocupa un espacio de 4 pies cuadrados, mientras que cada uno del segundo tipo ocupa 5 pies cuadrados. Si el propietario sólo tiene disponibles $2000 para su expansión y 26 pies cuadrados de espacio, ¿cuántos modelos de cada tipo deberá comprar y poner a la venta haciendo uso completo del capital disponible y del espacio?
Supóngase que el propietario compra x televisores del primer modelo y y del segundo. Entonces, le cuesta $300x comprar el primer modelo y $400y comprar el segundo tipo de televisores. Dado que la cantidad total que ha de gastar es de $2000, es necesario que
300x + 400y = 2000
Asimismo, la cantidad de espacio ocupada por los dos tipos de televisores es de 4x pies cuadrados y 5y pies cuadrados, respectivamente. El espacio total disponible para los dos modelos es de 26 pies cuadrados. Por tanto
4x + 5y = 26
Para encontrar el número de televisores de cada modelo que deberá comprar y poner a la venta, debemos resolver las ecuaciones para x y y. Es decir, debemos encontrar los valores de x y y que satisfagan a la vez ambas ecuaciones. Obsérvese que cada una de ellas es una ecuación lineal en x y y.
4.1.1 Definición
https://attachment.fbsbx.com/file_download.php?id=423111277899367&eid=ASuO0J_sXX9RSca5tdg6MUoSTv4uZTUbe0vEuDTAWalNO_Jy6E7LQU28D9qHdQtNZrg&inline=1&ext=1448417837&hash=ASvSehGp-_lUYlvB
4.1.2 Sistemas de ecuaciones lineales: consistentes, inconsistentes, y su representación paramétrica del conjunto solución.
matemprepa. (2014). Álgebra Intermedia - Lección 61 - B (sistemas consistentes, inconsistentes y dependientes). noviembre 30, de youtube Sitio web: https://youtu.be/k4JQQJdmmoA
4.1.3 Métodos para resolución de sistemas de ecuaciones lineales: método gráfico, igualación, sustitución, eliminación (sumas y restas).
Método de eliminación, de sustitución e igualación.
Método gráfico
TheNewNewton. (2012). Matemáticas E.S.O. | Sistemas de Ecuaciones: Los Tres Métodos. noviembre 30, 2015, de youtube Sitio web: https://youtu.be/UyV5EA3Pu5Q
julioprofe. (2012). Sistema de Ecuaciones Lineales 2x2 por Método Gráfico. noviembre 30, 2015, de youtube Sitio web: https://youtu.be/ieiRIATCOUI
4.1.4 Sistemas de ecuaciones equivalentes.

![\left\{
</p>
<pre> \begin{array}[c]{ccc}
x \, + \, y \, + \, z & = & ~~3
\\
x \, + \, y \, - \, z & = & ~~1
\\
x \, - \, y \, - \, z & = & -1
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{ccc}
x \, + \, y \, + \, z & = & ~~3
\\
x \, + \, y \, - \, z & = & ~~1
\\
x \, - \, y \, - \, z & = & -1
\end{array}
</pre>
<p>\right.](http://www.wikillerato.org/images/math/math-b4daf9b08947470816a091c908c8b878.png)
![\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~1 & ~~1 & -1
\\
~~1 & -1 & -1
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
~~1
\\
-1
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~1 & ~~1 & -1
\\
~~1 & -1 & -1
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
~~1
\\
-1
\end{array}
</pre>
<p>\right)](http://www.wikillerato.org/images/math/math-9d6156e83361678f19df40db3ecf5638.png)
![\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~0 & ~~0 & -2
\\
~~0 & -2 & -2
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
-2
\\
-4
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~0 & ~~0 & -2
\\
~~0 & -2 & -2
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
-2
\\
-4
\end{array}
</pre>
<p>\right)](http://www.wikillerato.org/images/math/math-45eb9fde313d2a75f1b05cd42aac6c52.png)
![\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~0 & -2 & -2
\\
~~0 & ~~0 & -2
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
-4
\\
-2
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~0 & -2 & -2
\\
~~0 & ~~0 & -2
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
-4
\\
-2
\end{array}
</pre>
<p>\right)](http://www.wikillerato.org/images/math/math-0730ab56aabea929252d49dbf9595acc.png)
![\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, + \, z & = & ~~3
\\
-2y \, - \, 2z & = & -4
\\
-2z & = & -2
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, + \, z & = & ~~3
\\
-2y \, - \, 2z & = & -4
\\
-2z & = & -2
\end{array}
</pre>
<p>\right.](http://www.wikillerato.org/images/math/math-eb6ec9bc0f3d4f3655e297c2d80271fe.png)
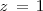
En la primera y segunda ecuación, sustituimos por la solucion de la tercera ecuación (
por la solucion de la tercera ecuación ( 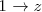 ), para obtener:
), para obtener:
![\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, + \, 1 & = & ~~3
\\
-2y \, - \, 2 & = & -4
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, + \, 1 & = & ~~3
\\
-2y \, - \, 2 & = & -4
\end{array}
</pre>
<p>\right.](http://www.wikillerato.org/images/math/math-5c98a4989cffb856e694abe6316e1767.png)

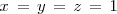







El propietario de una tienda de televisores desea expandir su negocio comprando y poniendo a la venta dos nuevos modelos de televisores que acaban de salir al mercado. Cada televisor del primer tipo cuesta $300 y cada televisor del segundo tipo $400. Cada televisor del primer tipo ocupa un espacio de 4 pies cuadrados, mientras que cada uno del segundo tipo ocupa 5 pies cuadrados. Si el propietario sólo tiene disponibles $2000 para su expansión y 26 pies cuadrados de espacio, ¿cuántos modelos de cada tipo deberá comprar y poner a la venta haciendo uso completo del capital disponible y del espacio?
Supóngase que el propietario compra x televisores del primer modelo y y del segundo. Entonces, le cuesta $300x comprar el primer modelo y $400y comprar el segundo tipo de televisores. Dado que la cantidad total que ha de gastar es de $2000, es necesario que
300x + 400y = 2000
Asimismo, la cantidad de espacio ocupada por los dos tipos de televisores es de 4x pies cuadrados y 5y pies cuadrados, respectivamente. El espacio total disponible para los dos modelos es de 26 pies cuadrados. Por tanto
4x + 5y = 26
Para encontrar el número de televisores de cada modelo que deberá comprar y poner a la venta, debemos resolver las ecuaciones para x y y. Es decir, debemos encontrar los valores de x y y que satisfagan a la vez ambas ecuaciones. Obsérvese que cada una de ellas es una ecuación lineal en x y y.
Arya., J & Lardner., R.. (2009). MATEMÁTICAS APLICADAS a la administración y a la economía. noviembre 24, 2015, de Departament of Mathematics, Simon Fraser University Sitio
4.1.1 Definición
https://attachment.fbsbx.com/file_download.php?id=423111277899367&eid=ASuO0J_sXX9RSca5tdg6MUoSTv4uZTUbe0vEuDTAWalNO_Jy6E7LQU28D9qHdQtNZrg&inline=1&ext=1448417837&hash=ASvSehGp-_lUYlvB
4.1.2 Sistemas de ecuaciones lineales: consistentes, inconsistentes, y su representación paramétrica del conjunto solución.
matemprepa. (2014). Álgebra Intermedia - Lección 61 - B (sistemas consistentes, inconsistentes y dependientes). noviembre 30, de youtube Sitio web: https://youtu.be/k4JQQJdmmoA
4.1.3 Métodos para resolución de sistemas de ecuaciones lineales: método gráfico, igualación, sustitución, eliminación (sumas y restas).
Método de eliminación, de sustitución e igualación.
Método gráfico
TheNewNewton. (2012). Matemáticas E.S.O. | Sistemas de Ecuaciones: Los Tres Métodos. noviembre 30, 2015, de youtube Sitio web: https://youtu.be/UyV5EA3Pu5Q
julioprofe. (2012). Sistema de Ecuaciones Lineales 2x2 por Método Gráfico. noviembre 30, 2015, de youtube Sitio web: https://youtu.be/ieiRIATCOUI
4.1.4 Sistemas de ecuaciones equivalentes.
Los sistemas de ecuaciones equivalentes son los que tienen el mismo conjunto de soluciones, aunque tengan distinto número de ecuaciones.
Obtenemos sistemas equivalentes por eliminación de ecuaciones dependientes. Si:
Todos los coeficientes son ceros.
Dos ecuaciones son iguales.
Una ecuación es proporcional a otra.
Una ecuación es combinación lineal de otras.
Criterios de equivalencia de sistemas de ecuaciones
1 Si a ambos miembros de una ecuación de un sistema se les suma o se les resta una misma expresión, el sistema resultante es equivalente.
2 Si multiplicamos o dividimos ambos miembros de las ecuaciones de un sistema por un número distinto de cero, el sistema resultante es equivalente.
3 Si sumamos o restamos a una ecuación de un sistema otra ecuación del mismo sistema, el sistema resultante es equivalente al dado.
4 Si en un sistema se sustituye una ecuación por otra que resulte de sumar las dos ecuaciones del sistema previamente multiplicadas o divididas por números no nulos, resulta otro sistema equivalente al primero.
5 Si en un sistema se cambia el orden de las ecuaciones o el orden de las incógnitas, resulta otro sistema equivalente.
vitutor. (2014). Sistemas de ecuaciones equivalentes. noviembre 3, 2015, de google Sitio web: http://www.vitutor.com/algebra/sistemas%20I/equi.html
4.1.5 Eliminación de Gauss y Gauss-Jordan.
MATEMATICAS EJERCICIOS RESUELTOS. (2013). SISTEMA DE ECUACIONES DE 3×3 METODO DE GAUSS Y GAUSS JORDAN PROBLEMA RESUELTO. noviembre 30, 2015, de youtube Sitio web: https://youtu.be/H7r9xAxbvg4
4.1.5.1 Definición de matriz.
Se denomina matriz a todo conjunto de números o expresiones dispuestos en forma rectangular, formando filas y columnas.

Elemento de una matriz
Cada uno de los números de que consta la matriz se denomina elemento.
Un elemento se distingue de otro por la posición que ocupa, es decir, la fila y la columna a la que pertenece.
Dimensión de una matriz
El número de filas y columnas de una matriz se denomina dimensión de una matriz.Así, una matriz de dimensión mxn es una matriz que tiene m filas y n columnas.
De este modo, una matriz puede ser de dimensión: 2x4 (2 filas y 4 columnas), 3x2 (3 filas y 2 columnas), 2x5 (2 filas y 5 columnas),...
Sí la matriz tiene el mismo número de filas que de columnas, se dice que es deorden: 2, 3, 4, ...
El conjunto de matrices de m filas y n columnas se denota por Amxn o (aij).
Un elemento cualquiera de la misma, que se encuentra en la fila i y en la columna j, se denota por aij.
Matrices iguales
Dos matrices son iguales cuando tienen la misma dimensión y los elementos que ocupan el mismo lugar en ambas, son iguales.
4.1.5.2 Expresión matricial de un sistema de ecuaciones lineales.
estudiia. (2013). Expresión matricial de un sistema de ecuaciones lineales. noviembre 30, 2015, de youtube Sitio web: https://youtu.be/Xn6TVlj2ilE
4.1.5.3 Operaciones elementales sobre renglones.
UTVPAV. (2014). Operaciones elementales de renglón. noviembre 30, 2015, de youtube Sitio web: https://youtu.be/y3F1B4-sVko
4.1.5.4 Reducción de Gauss y Gauss-Jordan.
Método de reducción de Gauss
El método de Gauss consiste en transformar el sistema dado en otro equivalente. Para ello tomamos la matriz ampliada del sistema y mediante las operaciones elementales por filas la transformamos en una matriz triangular superior ( o inferior ). De esta forma obtenemos un sistema equivalente al inicial y que es muy facil de resolver.
Ejemplo
La matriz ampliada del sistema de ecuaciones:
![\left\{
</p>
<pre> \begin{array}[c]{ccc}
x \, + \, y \, + \, z & = & ~~3
\\
x \, + \, y \, - \, z & = & ~~1
\\
x \, - \, y \, - \, z & = & -1
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{ccc}
x \, + \, y \, + \, z & = & ~~3
\\
x \, + \, y \, - \, z & = & ~~1
\\
x \, - \, y \, - \, z & = & -1
\end{array}
</pre>
<p>\right.](http://www.wikillerato.org/images/math/math-b4daf9b08947470816a091c908c8b878.png)
es:
![\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~1 & ~~1 & -1
\\
~~1 & -1 & -1
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
~~1
\\
-1
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~1 & ~~1 & -1
\\
~~1 & -1 & -1
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
~~1
\\
-1
\end{array}
</pre>
<p>\right)](http://www.wikillerato.org/images/math/math-9d6156e83361678f19df40db3ecf5638.png)
Si a la tercera y segunda fila le restamos la primera, obtenemos:
![\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~0 & ~~0 & -2
\\
~~0 & -2 & -2
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
-2
\\
-4
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~0 & ~~0 & -2
\\
~~0 & -2 & -2
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
-2
\\
-4
\end{array}
</pre>
<p>\right)](http://www.wikillerato.org/images/math/math-45eb9fde313d2a75f1b05cd42aac6c52.png)
Si ahora intercambiamos la segunda y tercera filas, obtenemos
![\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~0 & -2 & -2
\\
~~0 & ~~0 & -2
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
-4
\\
-2
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~0 & -2 & -2
\\
~~0 & ~~0 & -2
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
-4
\\
-2
\end{array}
</pre>
<p>\right)](http://www.wikillerato.org/images/math/math-0730ab56aabea929252d49dbf9595acc.png)
que es la matriz ampliada del sistema de ecuaciones:
![\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, + \, z & = & ~~3
\\
-2y \, - \, 2z & = & -4
\\
-2z & = & -2
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, + \, z & = & ~~3
\\
-2y \, - \, 2z & = & -4
\\
-2z & = & -2
\end{array}
</pre>
<p>\right.](http://www.wikillerato.org/images/math/math-eb6ec9bc0f3d4f3655e297c2d80271fe.png)
que es equivalente al inicial.
Solucionamos la tercera ocuacion para obtener  :
:
 :
: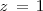
En la primera y segunda ecuación, sustituimos
 por la solucion de la tercera ecuación (
por la solucion de la tercera ecuación ( 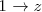 ), para obtener:
), para obtener:![\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, + \, 1 & = & ~~3
\\
-2y \, - \, 2 & = & -4
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, + \, 1 & = & ~~3
\\
-2y \, - \, 2 & = & -4
\end{array}
</pre>
<p>\right.](http://www.wikillerato.org/images/math/math-5c98a4989cffb856e694abe6316e1767.png)
La segunda ecuación es ahora una ecuación con una sola incognita,  , que resolvemos para obtener
, que resolvemos para obtener 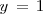 . Sustituimos, en la primera ecuación,
. Sustituimos, en la primera ecuación,  por 1 (
por 1 ( 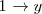 ). Esto nos da una ecuación en
). Esto nos da una ecuación en  :
:
 , que resolvemos para obtener
, que resolvemos para obtener 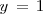 . Sustituimos, en la primera ecuación,
. Sustituimos, en la primera ecuación,  por 1 (
por 1 ( 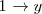 ). Esto nos da una ecuación en
). Esto nos da una ecuación en  :
:
que al resolverla termina de darnos la solución del sistema de ecuaciones inicial:
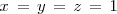
wikillerato. (2013). Método de reducción de Gauss. noviembre 30, 2015, de google Sitio web: http://www.wikillerato.org/M%C3%A9todo_de_reducci%C3%B3n_de_Gauss.html
Reducción de Gauss-Jordan
unicoos. (2011). Discutir un sistema 03 BACHILLERATO Reduccion Gauss Jordan. noviembre 30, 2015, de youtube Sitio web: https://youtu.be/klWAnkzOIbo
4.1.5.5 Sistemas homogéneos.
Si un sistema de m ecuaciones y n incógnitas tiene todos los términos independientes nulos se dice que es homogéneo.
Sólo admite la solución trivial: x1 = x2 =... = xn = 0.
La condición necesaria y suficiente para que un sistema homogéneo tenga soluciones distintas de la trivial es que el rango de la matriz de los coeficientes sea menor que el nº de incógnitas, o dicho de otra forma, que el determinante de la matriz de los coeficientes sea nulo.
r < n
Observemos que esto se debe a que:
De este modo estamos en el caso del teorema de Rouche en el que r(A)=r(A') y su valor es menor al número de incógnias, siendo así el sistema compatible indeterminado.
Ejemplos







r = 3 n = 3
Suscribirse a:
Entradas (Atom)













